
How
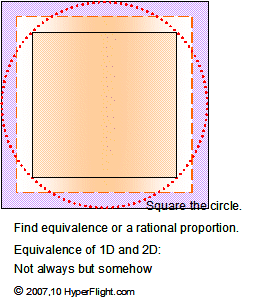
to Square a circle
Geometry
and its magic
Squaring (quadrature) of a circle unwinds a circle in an attempt of making the turns the same as straightaways
Making a circle out of a square is about reversible transformations of the circular geometry (2D, circle, compass) and the straight line geometry (1D, square, straightedge). Yes, we can figure out the symbols and the magic of Thoth
Pythagorean pursuit in squaring of a circle must be relevant and useful. Pythagoreans, then and now, apply math that describes the operations of nature. Squaring of a circle is about energy and its meaning is energy transformation
We put Euclid on the Pythagorean platform, too, for his fifth proposition is weak
So you take the circumference of a circle and make a square having the periphery that's exactly the same. Is there more to this than an intellectual exercise? Keeping your brain in gear? Proving something others said is impossible?
While it is commonly accepted that squaring of a circle is not possible, there are ongoing attempts to work this problem. Indeed, every person should understand what is behind the squaring of a circle because the implications of the process are richer than a philosophical discussion, a belief, trivia, or the plethora of various approximate constructions. To put it with a flavor of the East -- It's not about the destination, it's about the journey. Even though we are told that the answer at the destination is 'no,' we want to make the trip. As it happens, we will come to a fork in the road – a Pythagorean Y or a Greek Tau – which you will never find if you jump to conclusions.
A moving object has energy (technically called momentum) that is determined by its speed, which also depends on the distance the object is traversing (because speed is distance per unit of time). Going on a straight path the moving energy of an object has some particular value. If the curved path were to have the same distance as the straight path, the moving object's energy would be conserved at all times.
But what if the distance of a straight path cannot be the same as the distance of a curving path? The true question then comes up: Because the moving energy of an object is conserved, what happens to the object's energy if the path changes from being straight to curved? Similarly, what happens to the object's energy if its curving path is straightened?
The 'how to' square a circle is about the exact match in length because the energy is conserved exactly and if circle squaring is possible then the speed on the straightaway would be the same as on the curve. One way of seeing the 'straight' vs. 'curving' assignment is by taking a square and then turn the sides into flexible lines such that the circumference of the original square is the same as the circumference of the resulting circle -- or vice versa. This appears a simple thing to do and possibly in the recreational category, too. Applying the benefits of geometry -- and if its exactness brings something special to the table -- then geometry may well help us decide this question. In essence, if we can make the exact match between a circular path and a straight line path, then the moving energy is conserved and we could not use the parameter of energy to tell us the difference on what is straight and what is curved. But the straight line of a square and the curved line of a whole circle or an ellipse cannot be matched in length. Every time the geometry of a moving object changes between the straight and the curving, energy is released. The energy is released as force in the case of a gyro (really force times distance) -- or the energy radiates away or into the object.
|
We can also say that a tire will always leave rubber on the road even if we go perfectly straight because the 2Pi of the circumference is a transcendental number -- and no straight distance has the value of Pi. You will find the treatment of transcendentals on the Circle and Pi page while all incommensurable numbers are detailed on the golden proportion page. All is number! |
After a short
search on the Internet, the Ankh symbol is
nowhere to be found as being associated with the squaring of a
circle. But it is. Ancient Egyptians practiced and likely understood
magic as it is embedded in geometry and in natural life forms. (A
feather, for example, is both.) We are going to give the ancient
Egyptians a lot of credit for understanding their environment and for
dealing with complex topics such as the eternal life and the soul.
is
nowhere to be found as being associated with the squaring of a
circle. But it is. Ancient Egyptians practiced and likely understood
magic as it is embedded in geometry and in natural life forms. (A
feather, for example, is both.) We are going to give the ancient
Egyptians a lot of credit for understanding their environment and for
dealing with complex topics such as the eternal life and the soul.
Many interpretations of the Ankh center on sex and reproduction, particularly in connection with keywords such as life, the womb, and the phallus. Well, the reproductive mechanics are simple enough and it certainly would not explain why the ancient Egyptian gods run around clutching the Ankh. Reduced to the basic mechanics of sex, the horizontal bar on the Ankh could well stand in the way of doing it, too.
The square (straight, 1D) aspect and the curving (2/3D) aspect also deal with the intercept of cosmic energies and the Ankh symbol is about the human's fundamental geometric duality: the circle and the square -- the curving and the straight geometries. The rounded top, moreover, is not really a representative of a head or a body, but it is the round rib cage that expands during breathing. The air moving in and out (through your diagonal-passage nose, no less) is also undergoing a transformation between linear and circular/spherical geometries. It is nice to point out that Buddhists do practice and possibly understand this aspect of the "breath of life."
|
|
|
Mainstream math guys cannot advance the square-a-circle topic. To begin with, all math guys struggle with the reputation that they do not pay attention to applications. That is certainly the case. The easiest example is their treatment of geometric stars. Although they understand that some stars are constructible exactly and others are not, they do not know what to make of it, applications-wise. In the case of the squaring of a circle, many of them claim that the circle squaring puzzle is artificial, contrived, or useless. But of course, this is a super example of mainstream science logic: "If I should care about the applications even though I really don't, then I am safe if I say there exist no applications." On this page the squaring of a circle is tied squarely to energy and movement and atomic stability. But, really, don't expect the college professors to wake up one day just because you might have suggested the energy connection. It is within the individual person's ability and character to be fair and to challenge himself or herself. By not being able to deal with applications, mainstream science and math is for the most part irrelevant. By proving to themselves that the squaring of a circle is not possible, the mainstream science and math guys have completely foreclosed dealing with atomic construction and free energy -- and that's fine by me. |

|
|
|
From ancient Egypt comes a story of magic. The guy, or shall we say a god, in charge of magic was then Thoth, the Ibis-headed. He was also into records keeping because he was there when it was time to weigh your soul and that is when the truth and how much you did for truth is important. A point can be made that 'truth' and 'thought' are the two components of 'Thoth.' When Osiris Jr. was fighting to get his kingdom back he fought Seth and both inflicted heavy damage on each other. Osiris Jr. lost an eye. His compatriots were able to come up with pieces of it but could not get all of it. Thoth took what was left of the eye and restored Osiris Jr. eye through magic. No additional details are available.
You can have a field day finding geometric constructs on Thoth. Just a few: Hyperbolic cut on his skirt, diagonals across his chest and skirt, papyrus scroll as a cylinder. Are the markings on his arm one Royal cubit apart? Is the folded arm dividing the straight arm in the golden proportion? Is the folded arm making 36 and 2x72 degrees of the golden triangle? Why isn't the left hand thumb opposing the rest of the fingers? Is he making ellipses with his right hand fingers? Putting some of it together, consider Archytas using a cylinder to arrive at the doubling of a cube, which is necessary for the elliptical orbits (having the variable of radial distance the power of 3 and the variable of time the power of 2). Yes, Archytas needs transcendental numbers of the cylinder and that's what this page is about, too. [Let's do another one: I think the unclosed belt with the vertical axis of symmetry ("tail") is about the "tree hugging" posture in Tai Chi (has links to intelligent etheric energies).] |
|
Why did the Christian religion drop the ball and just kept the straight cross? After all, Coptic Christians in Egypt adopted the Ankh as their own symbol and a circle is also integral to the cross of the early Celtic Christians. A circle is quite difficult to understand and might be elusive -- and possibly painful -- even to the most ardent students of the Bible. The Ankh is also considered 'the key' to the eternal life and two keys are on the Pope's coat of arms. For the rest of the people (read followers), however, the Beast of Reduction has made his first mark: "Off with their heads. We will tell them what to think!" One key would be in the hand of a priest who positions himself in the gateway to your salvation. It is quite amazing how actively the Catholic Church wants their followers to stay away from a circle. So much so a circle is to the Catholics as a cross is to the devil. Perhaps a circle is the escapement from the dogma of the Catholic Church, a dogma resulting from a nice piece of marketing. It is really not that difficult to figure it out. Christ was given the crown of thorns, shown as a circle, and when you get into the meaning of a circle you will have to get over the thorns. Then there are the five wounds of Christ -- could hurt as you work the number five. And so it comes back from antiquity to the basic two questions:
|
|
The reproduction of species is an exceptionally complex affair. There is quite a functional difference between a womb and a vagina, for example, and all of the components need to be looked at with their geometric shape in mind. The function of the Couplex point is not understood at all but reproductively it is critical. (The Couplex is our English name for Chinese 'dantien' and Japanese 'hara' that is coined, explained, and applied in the Quantum Pythagoreans book.) |
Applying Pythagorean methods to square a circle, the goal is to take a one-dimensional straight line and convert it unambiguously -- that is commensurably -- into a multitude of zero-dimensional points because a circle is composed of points. Since a point is dimensionless and has no length, the conversion is not commensurable and not possible. In other words, you cannot take a point and measure distance with it. If you think this proof is simple, then perhaps that is how it should be. This proof is good for any curve such as an ellipse. However, this proof is a general proof. We cannot square a circle in general -- that is, a circle cannot be squared directly as a whole under all (arbitrary) conditions and under all circumstances, but that does not mean that a particular circular segment cannot be linearized.
This is more fundamental than you might think. When something can be unambiguously mapped back and forth from one state to another we can use the equal sign when we figure out the relationship. A complete one-for-one mapping between but two states such as 'potential' and 'kinetic' energy however, is not what usually happens in nature. We can force the environment to yield an equation but at the expense of doing it in a closed system. So we impose a lots of environmental constraints to get a two-way (equation-based) relation to hold but in the universe there are no such impositions taking place. Yet, the universe organizes nonetheless. If you wish to understand how things really happen, you will need to accept that a two-way back-and-forth mapping is an exception. The relations are normally over a multi-state (triangular or greater) processes, particularly if a transformation between the real and the virtual domains takes place, which means that the equal sign of algebra will not do. In our case, when we force to equate (use equal sign) between 'straight' and 'curving' to always hold, we will do so at the expense of tractability -- that is, the process requires an infinite number of steps and becomes intractable.
If you come up with a question, "Why would the infinite number of steps be intractable and bad while the infinite number of additions (superpositions) would not?," you are doing well. The "steps" happen in the real domain and each step takes finite time -- and therefore the infinite number of steps takes infinite time. Superposition is instantaneous in the virtual domain (and much of QM happens in the virtual domain).
 At
times the results of an analysis are easier -- and possibly more
effective -- to show in an art form. Yet, you'll have to know which
aspects are harmonious and which are disharmonious. If you don't feel
good (at the moment) you may get to like disharmonious designs. This
particular design on left deals with atomic construction and is
harmonious through and through.
At
times the results of an analysis are easier -- and possibly more
effective -- to show in an art form. Yet, you'll have to know which
aspects are harmonious and which are disharmonious. If you don't feel
good (at the moment) you may get to like disharmonious designs. This
particular design on left deals with atomic construction and is
harmonious through and through.
When
squaring a circle, every pebble on the road is a component of the solution
In two
dimensions the exact squaring of the circle through geometry or
arithmetic is not exact and so the squaring of the circle in 2D is
not possible. Even the Pythagorean Theorem does not do it. The
equivalence impossibility between 1D (square, straight line) and 2D
(circle, curve) shows nicely there is hard
separation between straight and curving geometries. In fact, the
impossibility of the squaring of a circle proves that the spatial
'straight' vs. 'curved' definition is not
by convention. Said another way, the straight and the curved are
individually enforceable. But you also know that the separation is
not insurmountable, for atoms with their curving orbitals and the
straight-line photons manage to interact in some exact way because
the conservation of energy holds. There then must exist a
transformative agent or agency. (For the ancient Egyptians it could
be god Shu, usually depicted with his arms at the diagonal.)
A spinning gyro can move in a straight line just fine, but how does the mindless gyro know the path is curving? A gyro has an angular momentum and an introduction of another curving -- that is angular -- momentum by the curving path is readily differentiated from the linear momentum. So it might be fun to work this anyway, for the squaring of a circle could be possible with, say, 3D constructs (pyramid?, angular momentum is always in 3D) or the transformative agent is an additional step we will have to go through.
The ancient Greek geometric constructions always call for a solution with a finite number of steps. The idea is that solutions that have some useful applications are those that are tractable. The point is that you don't want to deal with intractable methods, for they deliver solutions in some far away time in the future and only approximately at that.
You also do not buy the argument that it just might be okay to use intractable methods, for intractable methods would at some point yield an error that is very small. You do not succumb to the "small enough -- good enough" invitation, simply because you are thinking and working with energy. When applying intractable methods the result could be close all right, but because the energy is conserved you will not be able to explain what is happening with the energy's deficit or excess/surplus [and you may want to do better than Thoth, who chalks it up to magic]. When making a wooden round table you will finish in finite time and of course you are the practical guy who gets the job done. But now we are working with energy and that is an important context in its own right. [Yes, it is in your right brain.] You also feel that for the paths of a circle or a sphere the energies might be closely related to the atom because atomic orbitals have a curved and closed topology.
Here is where it gets a bit Zen (or metaphysical or alchemical). The Zen part is that now we got ourselves into quite a mess. We think we need to use tractable methods, for we want to be done by the end of the day -- but tractable methods are not available. Intractable methods do not help us with energy -- but working with energy is very useful. The only option open to us is to work with infinities while finishing in finite time! And for that we will need all components to be available to us right at the beginning -- the full infinity of them. And then we will need instant action. Well yes, we are entering the virtual domain of quantum mechanics where the waves do it instantly. (Okay, Bunky, what this means you'll hafta use your right brain.)
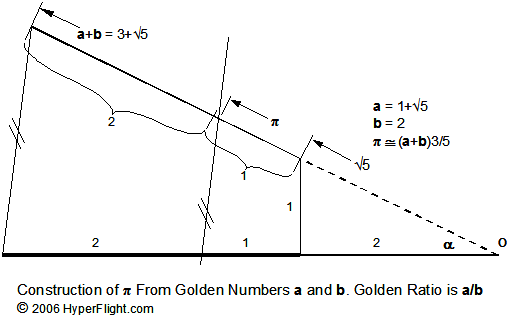
In the illustration above the approximate construction of Pi is that which is found in the Great Pyramid. (The angle alpha is on the golden proportion page with comments on the insides of the Great Pyramid.) While the Pi is approximate, you will need to figure out why the circle could be closed with it (think SQRT(5)). If you prefer the esoteric road, think "foam of Venus" to collect the infinities you need. Instant action will happen with QM superposition and that's doable, too.
When working the Great Pyramid you may begin to appreciate how the Pi and the proportions of golden numbers are tied together. You could start thinking it is one or the other but after a while you just might see their relationship.
Squaring of a circle is not strictly about the length equivalence of a circle and a square, for it is about reversible transformations between 1D-straight and 2D/3D-curved geometries. So, when you are working this you may also want to think about the exact division of a circle. You see, a section of a periphery of a circle (an arch or an arc) and its corresponding straight segment (cord) start and end at identical points. A particular curved section and the corresponding straight distance then also subtend the same angle. Such angle, moreover, could be an integer multiple of the whole circle. Multiplication or division by an integer or by a rational number is an operation that finishes in finite time, and that is the reason why the circle and the square could differ by a rational number while still satisfying the squaring of a circle goal.
If the proportion between the arch and the cord resulted in a transcendental number we could not use multiplication or division and finish in finite time because we would be dealing with an infinite mantissa and infinite computing time. However, if the proportion resulted in an irrational number, we could use the geometric mean to multiply out the irrational number in finite time even though irrationals also have an infinite mantissa [this goes beyond cool]. Bringing the ancient Egyptian fractions into this helps, too, for the components of the harmonics series represent energy components.
As a Pythagorean you want to think about the operation of multiplication and what physically arises from multiplication -- that is, how multiplication manifests in nature. Along the way you may encounter some universal constants as well.
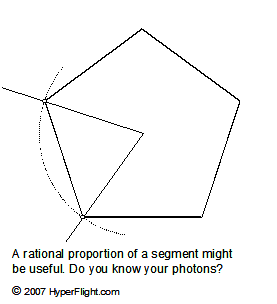
Now, the curving portion and a straight portion are in some rational or irrational relationship via the whole circle. Still, the paths (segment and cord) are not equal and the conservation of energy question comes up again. It's back to Zen but this time it is not that difficult. (Keep in mind a photon cannot be cut in two -- a minor complication.) The application here continues to be the atom -- its stability, energy extraction, and possibly gravitation. If you are a math guy, think Dirichlet. If you learned something about the hyperstar on this site, you can now also make a bet that all orbitals (energy clouds) must have a point (odd) or axial (even) symmetry.
Could we say that only some circles can be linearized -- and then in but a particular way?
Is this enough?
Atoms do
it every day.
If you want to have more fun, think about placing two circles (read orbitals) that would have their straight segments in a mutual rational relationship. Rationing is very Pythagorean. Yeah, you might need circumpositional numbers (that divide a circle exactly). Bring along the ancient Egyptian fractions, and you already know it's about energy. Happy thinking! Happy workings!
|
Also consider Euclid's definition of a point as 'that which has no parts.' Another way is through questions. a) "If you remove a point from a line, will its length change?"; and b) "If you remove a point from the inside of a line, will you cut the line?" [Just a couple of Western Koans from MI. Feb 2007] Note that the tasks of squaring the circle's periphery or the circle's area are equivalent. Proving or disproving one task is good for both topologies, for either topology is commensurable (proportional) to the other through a constant that is the radius. The picture showing the squared periphery looks a bit different than the one showing the squared areas, though (radius associated with periphery squaring is a bit larger). This issue is very similar to the difference between the momentum and the energy of a moving object. First formulated by Leibniz, momentum is proportional to v (velocity) while energy is proportional to v2 (a square number). Momentum and the moving energy of an object are commensurable with each other through v. The implication here is that the conservation of energy holds for the conservation of the object's energy as well as its momentum. (Quantum Pythagoreans book also talks about gravitational and energy vectoring and why momentum contains direction -- it's a vector -- while energy does not.) Just to make it a bit more complicated (but far more interesting), consider that the circle's circumference is, because of the Pi, a transcendental number. The straight distance of the square's sides can be either a rational or an irrational number because no straight distance has the value of a transcendental number. If a straight distance were transcendental we could solve for transcendentals with the Pythagorean Theorem. We cannot take the circumference of a circle that would result in a square (or a straight line distance) with a rational side (or a rational length), because the rational number has a finite mantissa while the transcendental number has an infinite mantissa. Now the question becomes: Can a transcendental number equal an irrational number? We answer this as 'no,' because irrationals issue from the Pythagorean Theorem (or an algebraic relation from among polynomials of any degree) while the transcendentals do not. Are we there yet? Almost. What happens if we ratio transcendentals and irrationals? This just might be it. That guy Pythagoras and his ratios are at it again! Rationing is not only about rational numbers, you know. [Would you rather be a Mayan, for Mayans had no fractions?!] |
|
Pythagoreans established rationing in the framework of musical heavenly spheres and in the harmony of tones. Using lengths of various strings, their ratios (proportion) resulted in particular harmonious and disharmonious sounds. But what if the length (1D) of a string keeps shrinking and becomes a point (0D)? Think infinity. Better still, think nonlocality. Best yet, think electron. It then also appears that rationing is an ongoing operation in nature and this could also point to the Pythagoreans' admiration for rationing. (Scientists in general think that Pythagoreans admired rational numbers but that just comes from their reductionist thinking.) Commensurable and incommensurable numbers take you on a tour from the finite to the infinite. |
|
The way of seeing the square-the-circle issue is in the context of transforming the linear geometry into curving geometry and vice versa, which is about the separation and coexistence of the Euclidean and Riemann geometries. The separation of the two is in the Fifth Proposition of Euclid's Elements where two parallel lines take the straight-only path. Riemann, however, opens the extra dimension by allowing a curvature. While Euclid's Fifth works fine for 'parallel' as two lines in a plane (think light beams), Riemann sees a sphere with longitudinals that, with identical curvature, converge and meet at the poles at finite distance where they close upon themselves (think atomic orbitals in a closed 3D topology). From the Fifth Proposition separates yet another, a third, possibility and that is of a line winding ("snaking") around a straight line, for both of these lines are equidistant -- just as parallel lines are -- but do not meet each other and do not close on themselves (coaxial or helix topology -- that is, open 3D topology). (All three aspects are incorporated in the Quantum Pythagoreans book from the Pythagorean perspective -- that is, each aspect has its representative in nature that meshes with its unique geometry.) The Fifth Proposition of Euclid, it is said, was difficult to formulate for Euclid himself. This proposition defines parallel lines and their properties. Euclid's difficulties point to his (and others') weak understanding of the Pythagorean concepts, which explicitly differentiate one dot (point, 0D), two dots (line, 1D), three dots (plane, 2D), and four dots (volume, 3D) geometries. The increasing number of independent dimensions provide different contexts within geometry. On top of that, each of the zero, one, two, and three dimensional constructs are individually enforceable. If Euclid were to say his 5th proposition is valid for parallel lines in 2D -- that is, in any plane, he would have been okay [this is what leads me to suspect that Euclid was a bit removed from the Pythagorean teaching]. Sometimes you can but oftentimes you cannot increase the dimensionality of the interacting geometry while holding your previous proposition valid -- and this is the basis of the group theory that deals with variant and invariant attributes. Variances are quite easy to see going from 1D to 2D, for example, but many people expect the 3D environment to be just a bunch of 2Ds stacked up like pancakes and essentially "the same." But there are many things around us that are naturally flat, including our solar system, and this is because tractable computing is easier in 2D. Carl "The Prince" Gauss knew there were deficiencies with the Fifth and encouraged Riemann to work this area. (It is a worthwhile exercise to see if the 4D environment is in some respects tractable and this is treated in the Quantum Pythagoreans book.) Another way of seeing the dominating nature of individually increasing 0, 1, 2, and 3 dimensions is that the numbers rule. In any beginning there is a number! Even today, challenges to the Fifth are summed up as 'non-Euclidean.' These challenges are trying to "unify" geometry by claiming that 'if another [my] geometry holds then Euclid is wrong [and I am right].' Not so. Simply said, the only diff between 'Euclid's parallel' and 'non-Euclid parallel' is that Euclid is valid in 2D while the rest belongs to 3D. It turns out that the addition of the third dimension allows two new constructs for 'parallel:' one for the open 3D topology and one for the closed 3D topology. In other words, the squaring of a circle is also an issue for the cubing of a cylinder and the cubing of a sphere. In 3D we encounter the problems of 1) Straight-and-round topology of a cylinder, which is in open 3D; and 2) Always-curving topology of a sphere, which is in closed 3D.{1 Jan 2007} The spherical, closed 3D topology is successfully addressed by Riemann while the cylindrical, open 3D topology is qualified but on this site (also see Touching in a Point). There is a way to resolve the squaring of a sphere as well as the squaring of a cylinder -- all in one swoop. It is closely linked to the interplay between the odd and the even symmetries.
|
||
|
Some people may run into difficulties and instead of admitting they do not have all the answers, they work hard to prove there exist no answers. Henri Poincaré is the case in point. He did not defer to geometry and claimed that straight and curving is, well, subjective. If we were to take Henri seriously, a gyro would have never been invented and perhaps not even attempted. Mathematicians and scientists make their proofs from assumptions and.. ..garbage in.. Okay, Henri's copout happened a hundred years ago. In 2007, though, a new vaccine had gone through clinical trials and is presently being marketed. This vaccine emulates a known cancer-promoting virus (or a cancer modality-morphing virus if you are closer to Raymond Rife) of the cervix -- yet the virus emulation is based in the geometry of the virus. No weakened virus or chemical similarities are present -- it is strictly the geometric form of the virus that supposedly triggers the human antibody response. If you know something about Raymond Rife's work, you would know that the geometric representation of the virus' benign form keeps the virus from morphing. The virus' geometric likeness is in the form of a virtual pentagon -- that is, the pentagon is hollowed out into a sphere rather than sticking out as a five sided object. This means the virtual pentagon will attract waves (energies) in the golden proportion, for a pentagonal real object (that sticks out) cannot form standing waves. Here might be a fertile ground for psychology. We could use a term for people who cannot figure things out and the way they compensate for it is by trying to dumb down the audience. The science writer who is clueless about the ancient Egyptian fractions then describes ancient Egyptians as simple farmers, for example. Einstein first dumbed down the audience by trying to show that the absolute motion is not possible, and then produced his feeble relativity theories. He denied ether only to work equations to his liking with miserable and miserly results. Could you go on a limb and say that brain functioning imbalance is due to poorly brain-formed geometric factors rather than the catch-all "chemical imbalance?" If our thought patterns have a geometric representation in the brain then this would make sense. |
|
Very common among scientists is the presumption that there is but one way of doing things. Actually, Euclidean and Riemann topologies exist side by side and both can be individually enforced. Transcendental numbers are the gatekeepers between the two [and she-dragons would make fine ones at that]. |
|
Archimedes was the first to apply a method in the calculation of the transcendental number Pi, which allows the computation of Pi to result in a large quantity of decimal places. Pi is the circumference of any semicircle (half-circle). Archimedes' method is intractable because we need an infinite number of steps (moves) to reach Pi. Methods or formulas by Leibniz and Newton that calculate Pi are intractable as well, and so is any other method that obtains Pi through the infinite multiplication/division of succeeding components. (Infinite addition can be accomplished in finite time through superposition but you'll need to be in the virtual domain.) But there is always but .. (think the golden proportion). The number of accurate decimal digits of Pi is not arbitrary because we will always run out of paper when trying to express Pi. Can we say that Pi is in some aspects inexpressible? Is such inexpressibility limited to real methods? |
While many books talk about Georg Riemann accomplishments, they are written mostly by mathematicians. (We've reviewed three books on Riemann.) Mainstream physicists bring up Riemann's magnum opus only to make a point about "curved space." So far, nobody differentiated curved space from curved pathways. So far, nobody applied Riemann work to atomic closed topology orbitals and to internal atomic tractability. It is for this reason the 0, 1, 2, and 3D geometries are not firmly anchored as discrete constructs for spatial behavior, which issue from the unique spatial tractability associated with each increasing degree of freedom.
|
Once you get into circle squaring you will encounter a plethora of derisive comments written about circle squarers. While you may go on knowing full well you are onto something, you will also encounter a new aspect of the human psyche nicely depicted as The Hanged Man of the Tarot. Some people get stuck (hung up) and full of frustration strike out at others around them. But you smile, for you just might find a way -- the Tau -- the others in the [this] life of them cannot. (Some Tarot decks have the Hanged Man suspended on a tree branch looking like a Tau.) |
|
About general proofs
Finally, a personal story. This is bit technical but the idea is that there exists a much engraved and authoritative proof regarding sorting that claims there exists the absolute minimum of NLogN operations to complete a sort of N elements. This proof is not wrong but it makes an assumption. In my (by now patented) implementation of the concurrent sorting process, the advantage is in realizing that even in a perfect random string some substrings (groups of elements) are sorted already -- that is, a perfectly random string does not have its elements always alternating high and low -- and sorted substrings can be captured right in the beginning. Suddenly the iron clad proof is not a proof, for there exists a several percent chance of a sort completing earlier than (the provable minimum of) NLogN while the new lower bound on sort becomes N. Moreover, everyday sorting deals with updates, which contain a previously sorted string and a new random string. Topics such as this are way too specialized and they are not in the Quantum Pythagoreans book. The idea, though, is that claims of a proof always rest on assumptions and you should feel free to question their relevance or applicability to what you want to do. There are no proofs without assumptions. The squaring of a circle is not possible in real-time using real methods. The part 'using real methods' is an important assumption and I've never seen it stated. There are plenty of infinite series (from Newton, Leibniz, Euler ..) that converge toward Pi. Now, the kicker is that when the components are waves -- that is, wavefunctions, the superposition (addition) is instantaneous and even an infinity of additions can happen in finite time. Assumptions issue from a context, which in turn is created in your right brain from an infinite number of variables. Context may be narrow or wide depending on your ability to construct larger or smaller time-invariant entities. Think self-organization and yes, the book gets into that. |
Go![]() or select another topic from the gold post
or select another topic from the gold post ![]()
HyperFlight home Portal
in new window
© 2007-13 Backbone Consultants Inc. Copyrights Information
Last update March 31, 2013
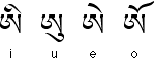 Would
you believe there is an alphabet based on the squaring of a circle? Yep,
it's that important. If the squarish dot in the center were to stand
for a zero-dimensional point then that would make sense. There may be
a bit more to it if you think the squarish dot has its sides in the
golden proportion.
Would
you believe there is an alphabet based on the squaring of a circle? Yep,
it's that important. If the squarish dot in the center were to stand
for a zero-dimensional point then that would make sense. There may be
a bit more to it if you think the squarish dot has its sides in the
golden proportion.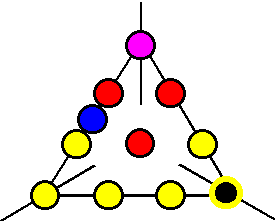

 A
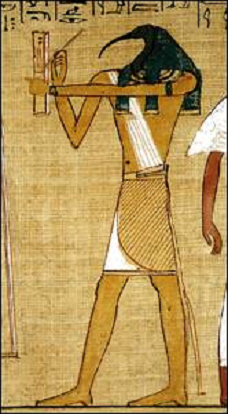
case can be made that the eye restoration story
is about the making of a circle from a finite number of components
which, moreover, requires some magic. Thoth knows a lot about
geometry and you can tell by the way he holds his arms. The beak of
the bird Ibis has a nice curve to it, too, and so you will not find a
compass sticking out of Thoth's pocket.
A
case can be made that the eye restoration story
is about the making of a circle from a finite number of components
which, moreover, requires some magic. Thoth knows a lot about
geometry and you can tell by the way he holds his arms. The beak of
the bird Ibis has a nice curve to it, too, and so you will not find a
compass sticking out of Thoth's pocket.

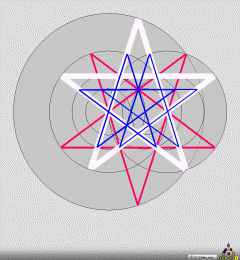
 We
have a collection of designs inspired by the five pointed star. View
We
have a collection of designs inspired by the five pointed star. View