Circle and Pi Really, now, what is Pi? Scientists with algebra do not have a handle on it			"A circle is a delimiter of context -- and it's not by convention." "What? Never heard of it." "That's the idea .. "
Circle and Pi, the definition You don't want to and you really cannot use the circular reference like the scientists; Easy to define Pi the Pythagorean way and it starts by drawing an arch of a semicircle. Yes, integers are in the definition and the operators show up when integers begin to move; Any and all circles share the same Pi Archimedes has figured out the Pi inside and out The semicircle of the Buddhist AUM is about the radial symmetry What is equivalence and what is reversibility Pi is more than was said by all, and it has to do with the even and odd symmetry. Actually, this is about the atom Pi figures in the conservation of energy. Ouroboros sums it up but not on a silver platter
Intro Everybody has something nice to say about a circle, as if a circle were perfect Carl Jung put a circle in the archetype category -- you have to go really deep to connect with it and a circle is something very basic and innate. On the other hand, many writers go straight up and call a circle a solar this or a cosmic that, possibly with the help of a shaman's drum. Geometers hang on to the equidistance from a point and use a compass when constructing a circle. This also results in a symmetry about a point -- a point being perhaps the most important geometric construct. Arithmetic works the point equidistance through a mathematical relation of the Pythagorean Theorem and by applying the horizontal and vertical distances in the Cartesian coordinates of Rene Descartes. Each point of the circle's periphery is computed and then displayed, and if you use random numbers the circle nicely fills in one dot at a time. The actual circle has an infinite number of points and we (have to) stop the computer when the circle is nicely visible. Or you can step through the angles and keep drawing the circle over and over. Math guys also like the stuff that has some periodicity in it because Fourier picks on repeating things very fast. For Pagans, a circle is the symbol of closure that has repeating periods, and from there it goes on to yet another harvest of nature's bounty and certainly a good cup of wine. You do not need to be a magician, here or in Tibet, to see a circle as the delimiter of context. A judge will make a circle around the case to make the universe of evidence admissible or inadmissible. When all descriptions of a circle are exhausted, some scientists give a circle another name such as infinity. Scientists tend to think of infinity as being stuck round and round in a rotary, and do not know the difference between unbounded and infinite. With recent Eastern imports a circle is zero and infinity, and maybe you should think which part is the good part before making a corporate logo -- Lucent and Vodafone coming to mind. All in all, we understand Pi from school as something to use when going from a straight line that is a diameter to a curved line of a circle, or vice versa. Once you understand how Pi is correctly and geometrically defined, you will also encounter the most interesting part about Pi and a circle: Pi cannot be made into a straight line. This is about the squaring of a circle and what it also means is that the transcendental numbers describing the Pi are different from rational or irrational numbers. Yet the scientists are wikkily (rhymes with happily) showing a wheel running over a flat surface claiming that one revolution of the wheel is the straight line on the road having the Pi in its length measurement. Not so. You are here to learn more than any scientist ever could. Not only that. You just might have fun with the scientists as you move on a path of the truth, directly or indirectly. The scientists' brain is left-centered, which means it is object-rich and relationship-poor. In one paragraph the ~wiki~ page named Pi shows the moving wheel producing the Pi on a flat path -- and right in the next paragraph the scientist talks at length about the impossibility of the squaring of a circle and speaks derisively about people working to square a circle. The scientist simply does not recognize the clear conflict in the presented information, for the scientist sees the two paragraphs as two separate objects and two separate topics. And this is just the beginning.. ..	While the real energy is well known as kinetic energy, the virtual energy takes some work. Free energy is about transforming the virtual energy into real energy. When squaring a circle we must reconcile the infinite transcendental numbers (incommensurables) with naturally finite numbers (rationals). The golden numbers make certain proportions that just might help with the infinite addition (superposition) of the virtual energy. The book you will thoroughly enjoy QUANTUM PYTHAGOREANS   More .. Leibniz (bio) first came up with an infinite series that adds up to a half of a circle's quadrant: Pi/4. Leibniz series issues from a trigonometric function and is the first real improvement over Archimedes' methods from 300 BCE that approximated Pi via geometric polygon construction. Let's say you ask 100 math teachers: "If Pi is irrational, how could you teach that Pi is a ratio (of C/D)?" How many of these teachers will answer with something similar to, " .. perhaps the format of the circumference-Pi relation for a circle is not clear."? Possibly one out of a hundred. How many will defer to a committee to fix it? All of them! Yes, algebra cannot do it but scientists do not mind reducing the task until they are just plain wrong while the teachers go along. This topic needs differentiation because division (or rationing) -- in and of itself -- does not always result in a rational number. The golden ratio is a ratio but it is not a rational number. You may want to take a look at the explanation of commensurables and incommensurables (both transcendentals and irrationals). A circle of diameter D could also be an irrational number but when you-the-builder pick up the compass and declare the distance between points to be of some length, D must now have a finite mantissa. This is crucial to universe (atom) building. One may argue that even God's tools become limiting to God, but a better way of looking at it is that reality -- if it is to remain organized -- is finite and God may wish to make reality that is organized. This logic has larger implications and even contains a gateway to gravitation. Think of gravitation as an extension to atomic construction.
Careful on how you define Pi. It may seem easy to do that but you want to be alert. Pi is routinely defined as the circumference C of a circle divided by its diameter D, and there appears nothing wrong with such definition in the scientist's mind. It is easy to paste the C/D = Pi all over the Internet and print it in books (even in books about Pi), but this kind of arithmetic is of limited use. Scientists say that Pi stems from an algebraic ratio between two numbers but the Circumference in the numerator is no ordinary number. It may not be obvious, but even if you measure the Diameter exactly and now you want to put the Circumference in the numerator, the circumference of a circle will not be exact because the circumference is a transcendental number. A trancendental number has an infinite mantissa, which is the sub-unity portion of a number. So, you cannot take a transcendental number with the infinite mantissa to start your computation to get Pi because this number does not fit in the computer to begin with, and there is not enough paper in the universe to write down one transcendental (or irrational) number. Pythagoreans also say that irrational numbers are unspeakable -- that is, nonverbal, as you would need an infinite number of words to express just one irrational number. Pi is not possible to define algebraically because Pi is a transcendental number, which cannot be obtained from an algebraic relation (that uses a finite number of terms). The best definition of Pi is through integers and radial movement (coming up). You will find you can obtain the numerical value of Pi -- or the circumference of a circle -- only by superposition (subtraction and/or addition) of an infinite quantity of components. Surprise, but Pi and the half-circumference of a circle (semicircle) are equivalent. They are the one and the same. Unlike the scientist, you know you cannot define a word by using the word itself in the definition (aka circularity of reasoning). Pi and C differ from each other by a constant D but because Pi and half-C are equivalent then you cannot use one in the definition of the other. Whenever you speak of Pi you also speak of a circle. Whenever you speak of a circle, you also speak of a sphere. Using a shorthand notation, the Pi and the circumference C of a circle would look like this: Pi equ C/D and also C equ D•Pi In math notation Pi C/D The equivalence sign (three horizontal lines) means that Pi and C are qualitatively equivalent and you cannot derive one from the other. It is not possible to explain, 'How to catch an elephant?' by saying 'Catch two and let one go!' If you have the cicle's Circumference you have 2•Pi•R (Pi•D) already. So, when the scientist says that Pi = C/D, he or she is saying that Pi = (Pi•D)/D and then Pi is defined as Pi. For a circle of radius 1 the scientist says that Pi is (Pi•2)/2 and then again Pi is defined as Pi. Scientists are not very smart and when they get together they herd together. The (infinite) addition mechanism to get Pi or Pi2 is substantively different from the procedure that generates the SQRT(2), for example, and this may lead you to suspect that transcendentals such as Pi and the irrationals -- really the straight-line incommensurables -- belong to two different classes of numbers. For starters, SQRT(2) is constructible with the Pythagorean Theorem in a finite number of steps, but transcendentals are not constructible with real methods in finite time, with or without the Pythagorean Theorem. This starts another chapter on Pi that deals with the squaring of a circle. The basic question is: Can the area or the circumference of a circle be equated exactly with the area of a square? You need to know the physical parameter represented by area to appreciate this issue.			We have two book reviews on Pi, both books authored by scientists. It is a sad story on what today's scientists can say about Pi. Semicircle and the Pythagorean Theorem leads to the construction of the geometric mean, which makes a square out of any rectangle and also solves for a square root of any distance -- even the irrational distance. We have a collection of designs inspired by the five pointed star. View select designs -- or visit our store at Zazzle (.com/Mike_Geo) and see how well you could look in a tee, a hoodie, or a long sleeve shirt. It is about being ahead of the crowd. All designs come from nature. The design on the right is called The Embrace but I also like to call it The Red White & Blue At The Court of The Yellow Emperor. Water and Salt design below.
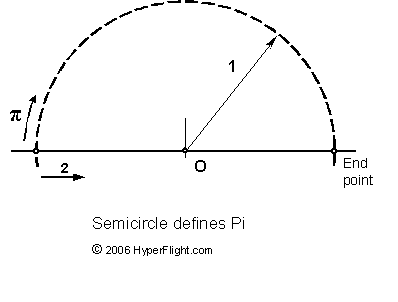
Easy definition of Pi, the Pythagorean way Now that we criticized the scientists' definition of Pi, we should offer our own, unencumbered, strict, literal, and unambiguous definition of Pi: Semicircle is a curve that has the unit distance of 1 from a point that that lies on a line. The semicircle has the starting and ending points on the line. At the starting point it is possible to traverse either a straight distance 2 or a semicircle distance Pi to get to the same ending point.
But of course, because the unit 1 can be of any size, Pi will always be Pi no matter how big the circle you come up with. Pi is created by a radial movement of the unit 1 and it is no wonder Pi is the same for all circles. The Pythagorean definition of Pi makes it easy to see that Pi and the semicircle are equivalent because the semicircular distance is Pi. The semicircular distance is the value of Pi. [It is also a nice definition because it gives you a choice. You can go straight in 1D to get to the ending point and you know exactly how far it is. Or you can take a more circuitous route where you'll get to meet the Pi.] On the technical side, Pi is classified as a transcendental number. There are also irrational numbers such as the square root of 2. Both the transcendentals and irrationals have an infinite sub-unity portion of a number. Transcendentals always exist in 2D while irrationals do it in 1D. This is our way of differentiating transcendentals and irrationals and you can read up about these two families on our page dealing with incommensurable numbers.			It is said Pythagoras started his studies with a semicircle. Not surprisingly, we need integers 1 and 2 to define Pi. Perhaps more accurately, we need the unit 1 and a doubling operator to arrive at Pi. You can get metaphysical here because 1 is odd and masculine while the even (2, doubling) is feminine. If you start with the length of 2, which is feminine, you will need the operation of halving to determine the point O at which to draw the semicircle. Halving is masculine. (Yes, cutting is masculine and you will find it in the left brain.) Self-referencing (or circular reference or circularity of reasoning) can be fun. Because a scientist produces a ratio of two distances that are inseparable to begin with -- namely the Circumference and Diameter -- the scientist profoundly announces that Pi is a constant. You can do one up on the scientists using self-reference when you say, for example: "Divide the number of cats you have by the number of legs they have -- and you will always come up with the number ¼. Therefore, the cats-to-legs ratio is a constant for small or large cats." So, how many cats do you have? That's easy. Add all of cats' legs and .. .. Ok, is Pi an exact distance or not? Because we can express Pi only with non-repeating and infinite number of digits (after the decimal point), we can argue that Pi is not exact; except that this is true in straight 1D geometry only. In a circular geometry, Pi is exact and only waves (wavefunctions) can achieve spanning the circumference exactly. Perhaps you can see in this the fundamental power of geometry from yet another angle. {June 8, 2013} You can also see it as a way of showing the impossibility of the squaring of a circle because the circumference of a circle cannot be equated with a finite (or irrational) number. However, it is possible that, going around the circle, some distance can become a finite (rational) number and then a particular segment(s) of a circle can be linearized. There is another 'however' in this. In orbital jumps we are concerned with the difference in two energies -- that is, the difference between two circles. Could the difference in two circles be linearized? This is about atomic sustenance and not about atomic construction.
What then is the actual value for Pi? There is an infinite series by Leibniz that is quite simple and it converges toward Pi/4 -- that is, this series converges to the length of one-half of a circle's quadrant. This formula is also the first qualitative improvement over Archimedes' method of "exhaustion," which uses inscribed and outside polygon construction to determine the ever-improving value for the circle's circumference of 2•Pi. From Leibniz: Pi/4 = 1/1 - 1/3 + 1/5 - 1/7 + 1/9 - .. This formula happens to converge to Pi very slowly. With an increasing number of new terms we get more accurate (closer to Pi) but -- compared to other methods -- the computer must do a lot of computing to show progress. Self test:-) If this paragraph does not make much sense to you, you are doing well. So, as a Pythagorean, you are not as much into expressing the magnitude of Pi on paper as you are into the actual construction and actualization of Pi. You start by seeing that the pluses and minuses can be implemented through superposition and in QM the superposition is instantaneous. Nice! In our definition of Pi we use 'distance' instead of 'length.' The straight distance is in 1D while the semicircle exists in 2D. Both exist in space (and all geometry exists is space). There are no restrictions on the diameter and the unit distance can be rational or irrational. That is, the unit distance is not limited to finite numbers such as rationals and this opens yet another metaphysical dimension. (Perhaps you understand now that the unit distance cannot be transcendental because it is always a straight distance.) If the unit distance were an irrational number the radius (and diameter) should be dashed because we change the context from unit length to unit distance but Pi will still be Pi (this is more important than you might think). Even Euclid thinks 1 is more than a counting number. On our Pythagorean page we have the Pythagorean Theorem working with circles aka loones.			Operators are well understood by the present day mathematicians (with a likely exception of i and minus 1). The treatment of operators is generally adequate and includes the null operator, which can be applied as having a body at rest (Aristotle would scratch his head on this one). The doubling operator is for some reason not included explicitly but there is, of course, the operation of 'multiplication by 2.' You will note that 'multiplication by 2' and 'addition of the same' arrive at the identical result but both of these are different operators because they represent different domains. (There is a tangent here on the golden proportion.) When you use words such as 'traverse' or 'measure distance,' you are describing a movement. In order to unambiguously define Pi, you need to get from here to there. It is the movement itself that uncovers the operators. Metaphysically, men at times need to make a pilgrimage or a quest in search of something. (In the book Quantum Pythagoreans the growth of the universe is accomplished through orbits, for the continuous accumulation of matter in a single body unbecomes tractable. The book explains why operators are forces.) Aetius iv. 2; Dox. 386. "Pythagoras holds that number moves itself, and he takes number as an equivalent for intelligence."
Archimedes
All topologies of a circle and sphere -- the periphery, area, and volume -- are equivalent to Pi through rational (exact, finite) constants. This is really a summary of Archimedes work from 300 BCE but [as you might agree] it has not survived in clean relations because of algebra. Archimedes also added the cone to the equivalence of Pi because he found a rational number that relates the volume of a cone to the volume of the cylinder (1/3). It is said he was very happy about that. The story has it that Archimedes had the cone volume formula inscribed on his tombstone. [While this story could be difficult to verify, a much better story would be that upon discovery he threw a great party and gave everybody a hat. The tradition of the cone shaped party hat would then have been started by Archimedes and it would also have become the longest surviving tradition in the history of the world. There. Then one guy built an arch in the honor of Archimedes and the world was never the same since. As you may well imagine, the guy called himself the architect.]			There is more to equivalence When Newton (bio) speaks of "equal and opposite force" (action-reaction), he is speaking of equivalence of forces that arise simultaneously and one (action) cannot exist without the other (reaction). Because forces are equivalent, one cannot arise before the other. Another way of getting to the same result is by understanding that all forces issue from the even (wave)functions. This is also the foundation of the action-at-distance because mass bodies separated by a distance act with the gravitational force that is equivalent. Yes, the earth is exerting force on the apple that is equivalent to the force apple is exerting on the earth. (Because the masses of the earth and the apple are in a huge ratio, the resulting acceleration will also be hugely lopsided -- but the forces are the same and pointing in the opposite direction. This is true of any and all forces -- such as when a photon is absorbed.) Action-at-distance is no big deal for quantum mechanics and this happens when the even wavefunction reduces: one big one for Newton. The gravitational wavefunction is an even wavefunction.
Reversibility of a math relation The equal sign of algebra signifies reversibility rather than equivalence, but this can be applied only in situations when there are but two and mutually exclusive outcomes happening over a single bidirectional path such as potential vs. kinetic energy (spring, weight lifting, pendulum) or pressure vs. volume (piston). It is easy to construct such bidirectional paths -- and the equations with equal signs to go with it -- in a closed system. But not all paths are bidirectional because at times the reversibility can be had only over a triangular path or a multi-state path having more than two states. For example, an absorbed photon can create several forms of energy. Some of the resultant energy quanta are not readily transformable back into photons and need to be worked over several stages before a photon could be recreated. Algebraic relation needs a bidirectional path for the equation to hold. So, while a bidirectional path can be created through a specific (closed system) context, a triangular path is a more general case found in nature. The kicker is that when dealing with virtual variables the system cannot be closed -- you cannot use real things and real methods to confine virtual variables. (You can use virtual methods but presently there are no guarantees and we usually speak of magic.) This also gets into intelligence and organization. The triad and tetrad of Pythagoras also indicate that the bidirectional path is not about the creation (of life, new materials, new systems, new abilities). Ancient Egyptians have several triads and quarterrnaries corresponding to various stages and methods of creation.
			In another example of algebra inadequacy, the equation E=m•c2 allows you to "calculate mass" of the photon by placing its energy on the other side of the equal sign. But a photon has no mass and then the algebra weakness is "explained" by calling the mass the 'effective mass,' while some algebra holdouts continue to hang on to a photon's mass and coming up with their own conclusions such as "tired" or slowing-down light. This equation simply and nicely shows that algebra is inadequate in general and incomplete in particulars. The equal sign works fine in the real domain where the commutative property holds (ab=ba). As soon as the virtual entities are encountered -- and light is a virtual entity -- algebra falls apart. This equation is incorrect in another way but the error discussed now is that irreversible transformations are paraded as reversible via the equal sign. Algebra is not representative of reality when transformations (reversible or irreversible) take place. [Einstein is a prototype for dumb and dumber.] Reversibility or irreversibility of a mathematical relation is an exceptionally important determinant and algebra needs to be replaced with another methodology. Presently, scientists muse about some of their weird or unusual results they get from their inadequate math while unable or unwilling to question math itself [think the left and the right brain].
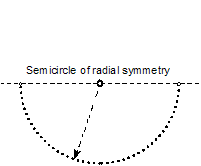
Semicircle in the Buddhist tradition There is a nice dot and a semicircle at the top of the AUM (or OM) symbol found in Buddhism. There are sparse interpretations of the AUM symbol, most of them deferring to the infinite, the unconscious, or to taking your own and individual path to its understanding. Because this site is about numbers and geometry, and because the numbers are at the heart of it all, we are not shy about delving into the aspects of the AUM, no matter how infinite and all-encompassing it may be.   <– "The best" The dot is indeed the nothing (indivisible, has no parts) as well as the everything (infinity). Because this dot is not real -- it is a geometric construct -- I prefer to draw it as a small circle. The dot is then infinitely small inside the small circle. It is through this dot the real and the virtual components are interconnected. This is indeed a big leap and so you may need to take it as a given for now. Intelligence in general is virtual energy and can be thought of as organized energy. One property of the virtual energy is that it is always symmetrical about 1D axis (the axis is not shown on the AUM). The total intelligence of the entire universe is symbolized by the component that looks like the number three on the AUM symbol. This is not the counting number 3 and neither it is a trinity but the two humps deal with the even, or axial, symmetry that is inherent in the formation of the virtual knowledge -- that is, intelligence. As you look through (or move through or think through) the dot you will extract, or copy, the kind of intelligence that is relevant to your needs. This, by now subjective, intelligence issues from the total intelligence of the universe and moves into the circle that could be you, for the circle is the delimiter of context. In Tibet, you could make the circle .. .. [yeah, make your own magic]. I'd put a little curlicue between the total intelligence and the circle to indicate spin (really a vortex). I'd also put horizon(tal) lines on each side of the point. If you are into the ancient Egyptian texts, think Aker. Oh yes, the semicircle. That is about reality, for all real entities have odd symmetry and that means that all real entities are always symmetrical about a point. You guessed it, it is the same point. You could interpret the semicircle in that you want to make something real from the intelligence you have received. You are still left with some unanswered questions such as "why is it a semicircle and not a circle," and "why is the horizon important and what qualitatively differentiates horizontal from vertical," and "where does Pi fit in," but now the answers are not all that difficult -- consider it your brainwork. In an advanced stage you want to develop the ancient Egyptian meaning of 'horizon' (horizon of fire,etc.) It's a thrill to arrive at some conclusion and then find a reference to Pythagoras that supports that -- in our case the idea of the 0D point and infinity being "the same." Before Aristotle criticizes Pythagoreans he writes (in Metaphysics):   "The Pythagoreans, however, while they in similar manner assume two first principles, add this which is peculiar to themselves: that they do not think that the finite and the infinite and the one are certain other things by nature, such as fire or earth or any other such thing, but the infinite itself and unity itself are the essence of the things of which they are predicated, and so they make number the essence of all things. .. .." There could be a tie-in between one Pythagorean idea and the AUM. Pythagoras is reported to have said something similar to: "The eternal world is revealed to the intellect [mind] but not to the senses." It is conceivable Pythagoras was teaching the freshmen and freshwomen from behind a curtain just to make that point. How do you make the sound of AUM? (Words are mostly about objects.) You start with A as a broad sound and imagine it as opening a book . This is the energy part. You are a smart person and you realize that the spine of the book is the vertical axis of symmetry. You transition to U as, of course, the semicircle. This tone then changes a bit as you go sounding ("curving") the semicircle. Pages of the book are now free to rotate about the axis. This is the charge part. Yes, the charge is always symmetrical about a point. (The charge and matter are closely linked. There is no matter without charge.) You move to vibrating M, where the spikes are the points that nail the two of the above components together in zero-dimensional points. The Latin letters fit in nicely considering the geometry and the associated symbolism. The Emerald Tablet is of an ancient origin that, while fully verbal, has its meaning purposefully obscured in alchemical language. Well, an alchemist would not say that their work is purposely obscured. Rather, an alchemist would say that the language of alchemy is condensed and symbol-association-based so much it appears obscured. And so it happens that we have the Tablet's interpretation on our Alchemy page. A circle and a sphere are made from a semicircle The starting and the ending points of both the straight and the semicircular distances are identical. A circle exists as the doubling of a semicircle and so the definition of a circle is also about the exact division of a circle by 2. Are there other numbers that divide a circle exactly? Or is it that any number can divide a circle exactly? You will need geometry to answer that. Metaphysically, the semicircle is feminine because the entire curve is symmetrical about the (vertical) axis. When making a full circle by, again, doubling, the 1st and 3rd quadrants become symmetrical about a point and, therefore, masculine. Metaphysically, then, "masculine arises from the feminine via the reflection about the horizon." If you get huffy about this, consider that masculine (feminine) is not the same as man (woman). If you still cannot get over it, don't go on a date with a witch. Perhaps the best application of a semicircle is the geometric mean. Because the geometric mean works for both the rational and irrational numbers, there are significant implications here to such (for some people esoteric) topics such as stopping moving bodies at a distance. Incidentally, since the geometric mean also constructs the square root, your attempt at achieving the squaring of the circle now includes Pi2 because you could then readily obtain the square root via the geometric mean. Pi2 has an infinite convergence series by Euler (if you want to give chase via QM superposition).
There is more to Pi and a circle Even and odd symmetry There are two basic functions applicable in the virtual domain of the atom: Even and odd mathematical functions. The property of the even function is that it is symmetrical about the vertical axis: f(x) = f(-x), while the odd function is symmetrical about a point: -f(x) = f(-x) (the equal sign means the author or the user of the equation thinks that the operation is reversible, and it is). The even function has infinitely inclusive properties such as those of a photon and it is an agreeable extension to call even functions 'feminine.' If the operation of translation or rotation have unique symmetries, then these operations can acquire gender as well. Inclusiveness is at times called superposition and it is truly infinite, not just unbounded. Generically, all even functions are forces [and may she be with you]. The odd function, you guessed it, has exclusive properties such as those of a proton and calling the odd functions 'masculine' then also makes sense because protons "butt heads" and displace each other -- at least in the real domain. Generically, all odd functions are real things, and bumpers with automobiles are just such things. Every atomic entity has properties that fit either the even or the odd function. The circle is the one and only geometry that has even and odd symmetry. This does not make a circle the gender neutralizer. Instead, because the circle is acceptable as both the even and the odd function in particular quadrants, the circle is the originator and the go-between among the two. The circle is the vehicle for the initial gender differentiation and the circle also facilitates the transformation between the two. There is a bit more here on the rotational symmetry associated with the five pointed star. Is i a number or an operator? Is -1 a number or an operator? i is a square root of minus 1. We know that -1=1/-1 but does the reciprocal of i equal i ? So, we take the equation i = 1 / i If you square both sides the equation is correct but if you multiply both sides by i the equation does not hold. If you try the above equation & non-equation on a real or self-proclaimed mathematician, chances are 99.9% he or she will not know where the problem is. You can tell him that squaring and/or multiplying both sides of an equation are both legal algebraic operations -- and chances are he knows it. Don't push it if you don't want to confuse the poor guy. (But of course, get him the book.) QUANTUM PYTHAGOREANS The Book There is much more to numbers than counting. With the i you enter the virtual domain and with it one of the largest chapters in the book. Continue ..			With the odd function you could begin to see how you could really explain the two-body collision mechanism. You will need to take the moving energy as a wave (easy) but then you will need to do a transformation. How can a circle become or stand for zero? You will need to visit India and learn how the zero came to be. Since a circle is the delimiter of context, the circle you draw can be evacuated of every real thing -- and you have zero. There are some who think this is not just an intellectual exercise because the circle can be emptied of real and virtual things. How can a circle become (or hold) infinity? This is a bit more complex than a simple reversal of the above. Think about and sound out the AUM, and go for it. Yes, you will need geometry. Transformation, as used by mathematicians, is not very transformative. The math guys see transformation as something that translates (moves, shifts) some function (a graph) along a line either horizontally or vertically to another spot. This just moves the reference and is not really transforming anything. Another form of transformation math guys claim is a transformation is to change the scale and this amounts to zooming in or out. Again, not very transformative. Finally, math guys speak of transformation when they flip a function about the axis and make a mirror image. You can easily see that none of these operations are transformational. For example, just because you shift from meters to feet as the new scale the math guy would say you are transforming but you know that the word 'transformation' should be reserved for something bigger than that. In our, that is Pythagorean, definition of transformation we speak of a change in the entity -- or the function describing such entity -- from the even to the odd function or vice versa. So, when a photon (even function) reduces by being absorbed, the energy is now converted to momentum that moves a couple of bodies such as molecules away from each other and the moving molecules now acquired an odd function as the two are moving away from a point. Similarly, when a real electron becomes the virtual electron it transforms from an odd function entity that is a real thing into an even (wave)function entity. (There is a bit more to this, for an electron has two components. Esoterically it is the Sphinx.) Dirac, a physicist and a mathematician, was pretty close and actually spoke of electron transformations. Incidentally, math guys are quick to point out that most functions are neither even or odd. What they do not say is that in the atomic environment there exist only the even and the odd functions. The reason is that only the even and the odd functions are transformable into each other, albeit in a non-trivial fashion. We have a couple of Pi stumpers you can try on your math teacher. Because math teachers subscribe to lame committee rules they are easy game.
Ouroboros In a simple and practical explanation, Ouroboros shows the difference between straight and curving geometry. If you have a string of some length then the expression of such length is always finite -- that is, the number that is the length of the string always has finite mantissa (it is a rational number). But the circle's circumference made from such string cannot and will not be of the same length because the circumference of any circle is not a finite number. The circle's circumference will always be shorter or longer than the length of any string. At times, then, Ouroboros is shown with excess or with a deficiency in the length of its tail. What this also means is that a circle cannot be made with a specific (exact) circumference because a specific number is a finite number and does not have an infinite mantissa. A more general case can also be made because a circle's circumference is a transcendental number and even the irrational number with an infinite mantissa cannot be made into a circle. Circles, ellipses, and other curving things are made from many zero-dimensional points. Because a geometric point is dimensionless, the number of points making a circle is infinite. Then there is also the question, "what entity can exist in the circumference of a circle?" By now you know it is not a real thing because no real thing such as a string can be made into a circle. If such curving entity is not real -- can it be virtual? If it is virtual -- does it exist? Can we see virtual things or entities? Does the electron become the virtual electron when it forms an orbital? Are dragons made of electrons? Some comment on Ouroboros as "eating its own tail." Perhaps you see now that such is not the case. Some could argue that the material can at times be transformed into virtual and that is the "eating" part. While technically true, it says nothing about the creation of the real world and why the creation of the real world prevails over its destruction. Continuing on, there is one other aspect of Ouroboros that shows up in the Mayan tradition. You might notice the Mayan dragon has seven segments. The number seven is the first number that does not divide a circle exactly and so there is a gap because seven wavelengths do not fit around the circle exactly. This has larger implicatons that are best explored via the Hunab-Ku symbol. If you think the "fiery breath" of the dragon has a link to a gap in a circle and consequent release of "free energy," you are doing well. You also want to be careful. The Christian aspect of control deals with the "slaying of a dragon" and your free energy work needs to be trully hidden (not just renamed). But of course, free energy is closely watched by any and all govt agencies.	There are also more esoteric interpretations of the Ouroboros. Skip the following if you don't fancy esoterica. Pi has an infinite amount of components calling for an infinite number of decimal places. You are pretty good if you asked a question: "What happens when its tail is chopped off?" Why, you could even discover there are different ways of drawing Ouroboros. As you look at all of them the Ouroboros of the ancient Egyptians looks the best, for it has a white belly on the inside. And then you might say: "Pi is a serpent? With scales or feathers, no less. Come on, get real!" My point, precisely. But this may all be too obvious and you do not see the woman. There must be a woman. "She is holding the sword .. vertically. There is a pivot, too." Yeah, the guy should be in charge of that pivot. But you can do better. "Engage the Couplex on the diagonal." There is not much to say.
Pi is also about nonlocal entities the likes of the electron Pi must facilitate energy conservation when entity's motion changes between the curving and the linear motion. Because Pi is transcendental then Pi's value is expressed with infinite quantity of components [here she is again]. The real domain, however, consists of object's values that have finite length (finite precision) that's just right for the real world. The curving geometry expressed by Pi is reconciled with the linear (straight) geometry of Euclid through some form of transformation. That's the importance of Pi and the basic differentiator between straight line irrationals and transcendentals. Talking about the squaring of a circle, eh? Talking about the nonlocality of an orbital electron and its 2D/3D energy. Pythagoras is likely to agree that classifying Pi as the transcendental number is a good call. If you wish to give a test indicating the level of understanding of physics by physicists, here is one question where the answer is not very encouraging. Ask any physicist: "Why would the Planck constant h be routinely divided by 2•Pi?" and he or she will say: "Because it is convenient." Yikes! We are almost there. The classification of some numbers as 'transcendental' presents a very old challenge. All non-transcendental irrational numbers the likes of the square root of two are readily constructed with the Pythagorean Theorem. The transcendentals, however, take you for another and altogether different ride. A circle can take you places. Possibly the longest unanswered cry is that of Archimedes: "Give me a point and I will move the earth!" Is there such a point? Such fulcrum? Is it a fixed point or is it a geometric 0D point? Ah. Think golden proportion. Now that we created the circle, it may be fun to explore the exact division of a circle. Some numbers do it, some don't.			QUANTUM PYTHAGOREANS  Book by Mike Ivsin If an atomic component changes from linear to radial geometry, energy imbalance arises because linear and curving paths cannot be exactly the same. The atom maintains its stability by radiating or absorbing energy to or from the environment because the geometric transformation must be energy-neutral. Quantum Pythagoreans describes linear and curving topologies, and the sustenance role of light for the two topologies. The pyramid then also provides the geometric constructs for the creation of new matter and for healing too. The duality of the real and virtual energies is not only introduced but is fully developed as two interacting domains. Continue ..
Go or select another topic from the gold post HyperFlight home Portal in new window © 2004 -- 2013 Backbone Consultants, Inc. Copyrights Information Last update June 8, 2013