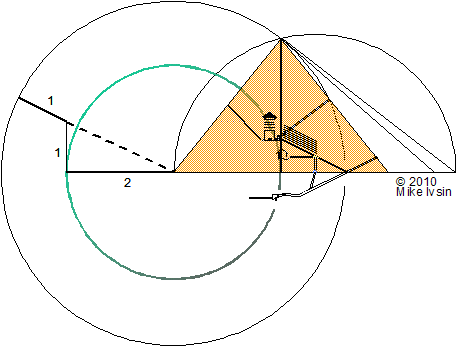|
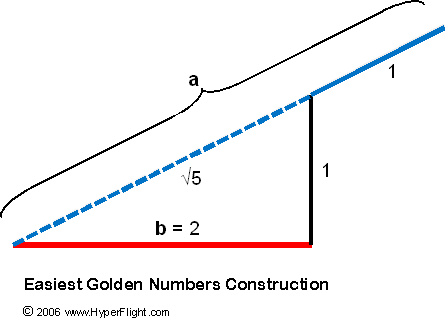
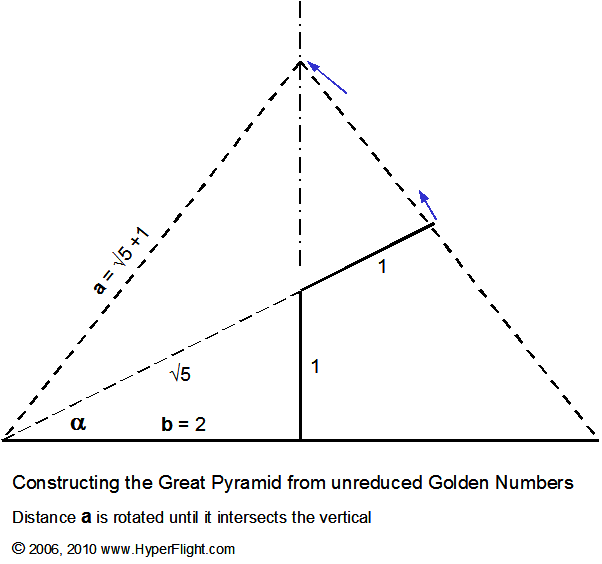
We are going to call the spatial
distance SQRT(5) + 1 the number a,
and the length 2 the number b.
The number a is irrational but tractable in geometry. This is
important, particularly since the same cannot be said through
arithmetic or algebra. Also, we are not reducing the number b
to 1 and b then remains at 2. In the Pythagorean
tradition, 2 is "not really a counting number."
Well, 2 is best thought of as doubling or the octave.
Try thinking of 2 as an operational verb, too.
Number 2
(or half or doubling) is prominent in symmetry about axis and gives
unique properties to all atomic even functions. You could reduce all
even functions because they can all be split in half, but all even
functions exist as even
functions until they are actually
reduced. This sounds like a riddle but it should not be if you are
familiar with QM.
It is a riddle if you think of the number 2 in metaphysical terms[,
and you might have a tempest on your hands if you try to reduce her].
It's okay to reduce even functions, though at times it might not be
the best thing to do. (There are some hot ways of going about it,
especially if you are in the land of the snows. There, you will need
to break out another "number 2" —
duality in geometry.) [In the ancient Egyptian context think Seth and
one of the reducing tools he's using.]
We are now ready and define the
golden ratio as the unreducible ratio a/b. In the formulation
with the SQRT(5) or in
its geometric form the golden ratio is exact. At times the golden
ratio is also called the divine ratio or divine proportion and once
you discover some additional applications you may give it the name
the likes of "the fulcrum of the heaven and the earth"
— perhaps in the same spirit as the cry of Archimedes.
The reason you do not want to
reduce a/b into one number [and call it Phe, Phi, Pho, or
Phum] is because the exciting relations are not confined to a/b,
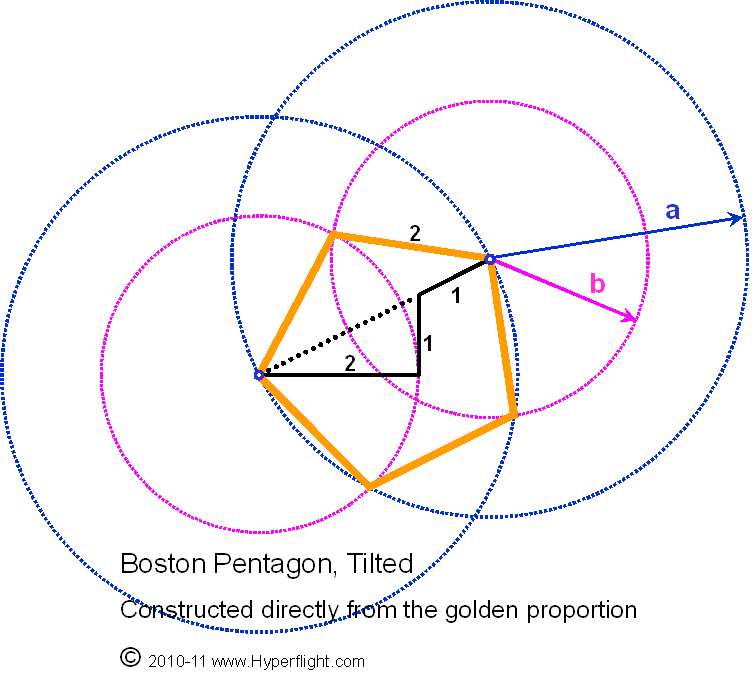
but also include a+b, for example. A good
start is a·b, which is the area of the
golden rectangle having close association with Balmer's
atomic orbital sequence. In the Great Pyramid the relations between a
and b are even more striking. For triangles
alone the golden numbers construct three different triangles
when a and b are used for sides, base, and height. On
these triangles the golden numbers in different spatial positions
then produce three different answers corresponding to three different
angles while arithmetic produces but one
answer (and this is a good example of the disadvantage of reduction).
Therefore, keeping the golden numbers unreduced and staying with
geometry will allow us to appreciate all proportions of these great
numbers. Saying 'golden proportion,' then, is more descriptive than
saying golden ratio (or golden mean, ~ section, ~ cut,
~ rectangle — or the mean and extreme
ratio). It all starts with the golden numbers. What proportion or
what relationship you chose is in the realm of your applications, be
it atomic construction, architecture, economics, on your Valentine's
card, [or on our Tshirt].
Composing and
working the Great Pyramid, we want to keep the denominator of the
golden ratio at the unreduced number 2 because the number 2 in that
case stands for the octave (doubling).
In the beginning we came up with
one golden numbers relation
a/b =
b/a + 1
and this relation is also better
looking than doing it with Phi. [Just because the ancient Egyptians
did not wear your phunny hat does not mean they knew nothing of
hats.] When a/b is used as a multiplier in our banking
application we need to subtract 1 to obtain the identical
adder. When we subtract 1 from the golden ratio a/b we
get b/a, which is the reciprocal of a/b. Could this
yield a more succinct definition of the golden numbers' property?
Besides, the reciprocal is sooo important, particularly if you ask:
"What is the reciprocal of a wavelength?"
Another interesting formulation
with the golden numbers is
a2 – b2 = a·b
which relates the squares of
golden numbers through the area of the golden rectangle. Big deal?
You bet. The left side is the Pythagorean Theorem that takes the area
of the hypotenuse and subtracts from it the area of one side of a
right angled triangle -- and that produces the area from the last
side of the triangle. Take a look at Balmer's equation and spice it
up with the geometric mean. (Forget Bohr, for he had corrupted it
through reduction.) It is even bigger if you, as a Pythagorean, know
the physical representation of multiplication in nature.
And the Pi
Some people claim
the number Pi is built into the Great Pyramid in various very close
approximations. On this page we show (below) that the golden
proportions are in the Great Pyramid as well. Now, if you use the
golden numbers a and b in the expression
3·(a+b)/5
you will get to Pi
to within 15 parts per million. If you get involved with energy —
either as it relates to your body or as it can be freely harnessed or
by analyzing the crop circles — every time
you work the golden proportion you will also be working with the
SQRT(5). Because the golden numbers are soo close to Pi, you will
inevitably think you are working the quadrature
of a circle. And quess what: you are.
So what's the
tie-in between the golden numbers and Pi? The golden number a
contains the square root of 5, which is the irrational number
while Pi is the transcendental number. The following section
is about these two kinds of numbers and .. well, think about the
physics entities that subscribe to these numbers. We'll be in the
micro (atomic) and it's a good intro to the squaring of a circle. Yes
of course, irrationals span 1D while transcendentals curve in 2D. |
|
What? Number 2 not
a number? Pythagoras started counting at number
3. This is not because numbers 1 and 2 are not really numbers (they
are), but it is because there are so many things that apply to 1 and
2 besides just being a count -- numbers 1 and 2 are best thought of
in such prevailing terms [and you don't want to get carried away
counting pebbles on the beach]. We need integers 1 and 2 to
define the Pi of a circle.
In another example, Planck constant
is the smallest quantum of energy that is used inside the atom as the
smallest increment within the orbital, while Balmer's
relation deals with integer energy increments between
orbitals. Planck constant and Balmer's orbital numbers are important
energy units that should stand outside of the counting number
1. As a Pythagorean you construct the monad as a commensurable
entity. (The smallest monad is the atom.) Having a monad as a real
thing, you then start the count using the monad as the object 1.
As a Pythagorean you should not have difficulty understanding that a
monad is composed of other numbers but as a real thing it becomes the
object 1, which is now a counting number 1 as well.
Natural numbers
can be used for counting but they are not just counting numbers.
There are odd
functions inside the atom as well; odd
functions describing symmetry about a single (one) point.
There is no symmetry about volume (3D) but then the number 3 starts
the count as the monad, which is the first stable (and
countable) thing. If you want to be mysterious about it you
might say "three is one." See Pythagoreans.
Academia loves to
discuss precedence. Some even go as far as to
say that the Pythagorean Theorem is not original because it is
preceded by number triplets from Mesopotamia such as 3, 4, 5. Yet
there are two original aspects to the Pythagorean Theorem: 1) The
establishment of a (square) relationship between the triangle
sides and 2) The result of the relationship yields both the rational and irrational
numbers -- that is, the Pythagorean Theorem is valid for any
conceivable distances of the right triangle sides. (That is how
Pythagoras or Pythagoreans discovered irrational numbers. There is
additional discussion about the Theorem
on the Pythagorean page.)
Any writer could
pretty much make any point he or she wishes.
They can put together quotes from Aristotle and Plato and Archimedes
and Newton .. and make a claim that some concepts are old hat. There
is a lot of context shifting and translation gymnastics going on,
too. Well, nobody really jumped up on the Pythagoras' concept of starting
the count at 3. Nobody was really interested in usurping this
very strange idea and it continued to be attributed to Pythagoras.
Once you understand the reason behind it you will see the true
originality and the depth of Pythagoras. All is number. |
|
These reductionists! Well, don't
worry about them. They pose greater hazard to each
other than to the rest of us. It's okay if they do the mind job on
each other and only on each other. So you still have the burden of
figuring out who si who and what is hwat, for reductionism is about exclusion.
The reductionist
"simplifies" a particular thing by discarding or ignoring
some apparently inconvenient components. Take
the concept of 'space.' Because 'space' is such a loaded (grouped)
term, several people can take different positions and, by discarding
certain aspects of space, "prove" what they want to prove.
You want to differentiate
space
into distance and length and degrees of independence. Distance is
the 1D construct of geometry while the length is the measure of
something real. You can then discuss how (or if) you can transform
distance and how distance can become a dependent (subordinated)
parameter when you transition into the virtual domain. Yes, this
seems complex but now you can make some progress and even get
there from here.
Another example of
reductionism is 'the field.' Without defining a
field you can become a science writer on it but once you try to
define it and differentiate it you will see there is no field without
geometry. A field, in and of itself, is great for your vegetable
garden. To make a linear field, for example, two flat parallel plates
need to be manufactured and placed in position. Speaking of a field
without saying how it is created is not even wrong.
A nice example of
an attempted reductionism is the 'straight' vs 'curving' path
(or motion).
Mathematician Poincare simply said the straight and the curving is
subjective. He did not bother to differentiate the two and likely had
no clue on how to do it objectively. Although ancient Greeks thought
of the curving lines as godly, Poincare took the easy way out and,
well, he was dead by the time the mindless gyroscope was able to tell
one from the other.
The best example
of reductionism is the relative vs. absolute motion.
The 'cannot tell the difference' reduces the logic by grouping
concepts together but it corrupts reality. But of course you can tell
one from the other via the quantum
mechanical dual slit experiment.
The biggest
example of reductionism is the taking out of ether.
It's okay if you think it does not exist but
make it your own belief and pursue it on your own nickel. If you want
to convince me ether doesn't exist I know better and want my money back.
In a case of the
Newton's term 'corpuscular,' the present day
reductionists equate this word with 'material.' This is a wonderful
example of trying to reverse the differentiation, for Newton
understood matter very well and because he knew that light
is not the same thing as mass he differentiated light from mass
(materia) by calling it corpuscular. Even today, corpus or
corpuscular is not just about something physical -- a 'body of
knowledge' aka corpus, is a collection of intangibles in a particular
context. Corpuscular is best translated as 'embodiment' -- something
cohesive that hangs together logically. In a context of light,
embodiment is intangible and based on waves (wavefunctions) that in
turn are based on the square root of minus one.
A recent case of
reductionism comes from Richard Feynman. In his
theory he needed to have the subatomic environment a collection of
billiard balls and so he reduced electrons and photons into just such
little critters. Consequently he could not explain the dual
slit experiment and spent a lot of time musing about it, making
his musings run into 'not possible to explain,' as if he were a guru
rather than a guy who is just clueless. Actually, when he reduced an
electron into a local and well defined object he jumped right into
intractability of 'all possible path histories.' That is what happens
when you ignore or deny the "inconvenient" nonlocality of a
wave or, in case of Feynman, do not know what to do with waves. If
you are a scientist you'll see right away Feynman is in a
self-induced non-polynomial (NP) and intractable attempt hopelessly
bogged down in the musings over the traveling salesman problem (and
under finite time constraints to boot).
A reductionists
agenda is to reduce you. One of his or her options is to ignore
pertinent stuff and insult the audience. Mario Livio
in his Golden Ratio
book calculates the theoretical golden ratio and the actual
face-to-half-base ratio of the Great Pyramid -- and finds the
difference at 0.1%. Because he doesn't know the purpose of the
golden ratio, Mario flatly states there is no connection between the
Great Pyramid and the golden ratio. Livio first compiles a lot of
stuff but when it's time to deliver he slams the reader with crap [it
is a form of a betrayal]. Livio must ignore the well known crease
running the mid-face of the pyramid and insults the reader with 0.1%
arguments. "Glowing reviews" is the hurdle you have to
overcome. There are many authors, including myself, who do not seek
one-liners for the book's back cover, for these mini reviews are
available for a price.
Reductionists also
parade as skeptics, debunkers, and bad news bears.
Reductionists'
motivation is simple. Reduce the answers to those few that can make
money for but a few. Medical treatment is a good example. Yes, we
want health care but if the reductionists were to have their say the
alternative and in some cases revolutionary medical treatments would
not be covered by insurance. Most of the time the treatment is simply
disallowed. You guessed it, reductionists are in the infrastructure
and alternative treatments are not making money for them. Another
case is in sciences. Totally worthless projects are being funded
after the physics has been corrupted and reduced into trivial and
irrelevant pursuits: big bang, black holes, dark matter and
dark energy, gravity waves. But you are really smart. You trust
doctors and hospitals and can afford healthcare premiums -- and big
bangs to you have nothing to do with NASA. Yet, maybe, you want to
check your retirement portfolio. There may be assets in there the
reductionists deemed adequate. These assets do not trade on the open
market and they have some value some experts put on it after getting
some fee for it. Housing securities got you reduced? Oh, the
portfolio managers' cut is long spent. It sure got the whole country
reduced. When you finally figure it out [while you have a choice],
invest yourself in free
energy. It is not as easy as free speech [today, in the US] but
you will never be, you don't want to be, and you don't have to be, in
the company of the reductionists.
Bob Lazar worked
to reverse engineer UFOs but his statements regarding the inadequacy
of our present knowledge are not reductionist.
His willingness to express and explain the alien technology with his
MIT and CalTech vocabulary nicely shows his misconceptions of reality
in general and physics in particular. Bob and many like him have
great difficulty integrating and applying new knowledge.
Nevertheless, Bob is not trying to reduce and "fit the new
reality" into existing limited-by-reduction mindset -- and
that's a good thing. He'd rather look silly than explain it away --
and that's a great thing. Except that now you have to figure out why
he did not find any cables in that thing. |
|
|
The irrational distance always
exists in 1D because it exists between two points --
such as the often quoted square root of 2. To get to the SQRT(2) we
need rational lengths and a 90 degree rotation to construct it --
that is, we cannot get irrationals by staying in 1D. (You cannot get
any irrationals through arithmetic -- see below.) So, here is where
the Pythagorean Theorem comes in: We construct rational distances
(1D) and open up the second dimension by making the right angle. We
use areas (squares, lunes -- that is, 2D) to obtain the relationships
and then move back to 1D via the square root. Relying on the
Pythagorean Theorem, the distance presented across the diagonal contains
the square root already. This serves as a nice intro
to the computational power of geometry. In general, the square root
is constructed through the geometric mean. In the Great Pyramid the
geometric mean is its height.
As a mainstream
math guy you might have thought the above
description of moving from 1D to 2D and back is not very exciting. As
a Pythagorean, though, you know what the 2D domain is about and so
you know what physical (and physics) parameters you will be dealing
with when working the irrationals. |
|
As a Pythagorean
you understand Tetractys as not only
representing but actually being the 0, 1, 2, and 3 dimensional
constructs that exist within geometry [advanced]. Now, the 0D (a
point) is routinely ignored although it is a unique and very useful
geometric construct. (It is not ignored in the East, though, for it
is well understood as Dantien/Hara. Quantum Pythagoreans book
tells you why a point is critical and why some versions of the Tao
symbol include dots -- that is, points.) You might think the
reductionists were busy erasing the geometric point as a unique
dimension in its own right. The reductionists, you might think,
deleted the dimension zero and replaced it with time as the fourth
dimension. Not so. Reductionists are simply not that smart. The four
dimensions issue from Tetractys as the Tetra (Quad) of 0D, 1D, 2D,
and 3D. Time is always a dependent variable and cannot become
independent as the degree of freedom is. The reductionists are really
rather dumb and you just want to stay on track while keeping an eye
on possible corruption. A case can be made that reductionism is
limited in the creative dimension and, technically, a reductionist
will always be corruptive in the long run. So what kind of degree
of freedom does a point provide? Rotation, orbits, orbitals, spin
-- all the angular stuff. Selftest:–) How much of the real
moving energy in the universe exists as rotation and orbits and spin?
About 99%, give or take a percent.
What is the
significance of the golden proportion? What is
the deep meaning of it all? Well, how deep do you want to get? The
gateway is really about the knowledge of the mathematical
representation in Nature. As a Pythagorean you want to know the
representation of an area (2D) in the real physical environment.
Nobody [as far as I know] understands that the Pythagorean Theorem
takes you from 2D to 1D and vice versa via the square root. (Get with
it -- our solar system is flat.) Then you want to know how Nature
performs addition and subtraction. Finally, what is multiplication
and how Nature does multiplication? It is a simple synthesis after
that. {April 2006}
Why, for example,
is the golden proportion concerned with the balance between
multiplication and addition? What is the
purpose of adhering to these operators while keeping them in balance?
Operators arise when numbers begin to move such as when dealing with
the trajectory of a circle. The multiplication and addition apply
(come from) two separate domains -- real and virtual -- and they need
to be in balance. Quantum Pythagoreans book deals with these
domains in both the direct and indirect fashion. The idea is to find
numbers and operators as the elements of Nature. |
|
QUANTUM
PYTHAGOREANS
The
book of numbers and stars and operators
Ready
to understand the stars, the pyramids and how the octave fits in?
What happens to energy when it encounters the pyramid geometry? How
harmony and disharmony relates to rational numbers and circular geometry?
Continue
.. |
|
Self test:–)
If you think Phi is useful, try expressing the area of the golden
rectangle a·b using Phi (Phi is a/b
and the usefulness of a·b
is described in the left column). If
you don't succeed you will be able to see why the ancient Egyptians
did not use Phi but used the golden numbers a
and b in all kinds
of geometric or arithmetic relations. You are now ready to look
unreduced and unburdened into the insides of the Great Pyramid in the Quantum
Pythagoreans book. |
|
|

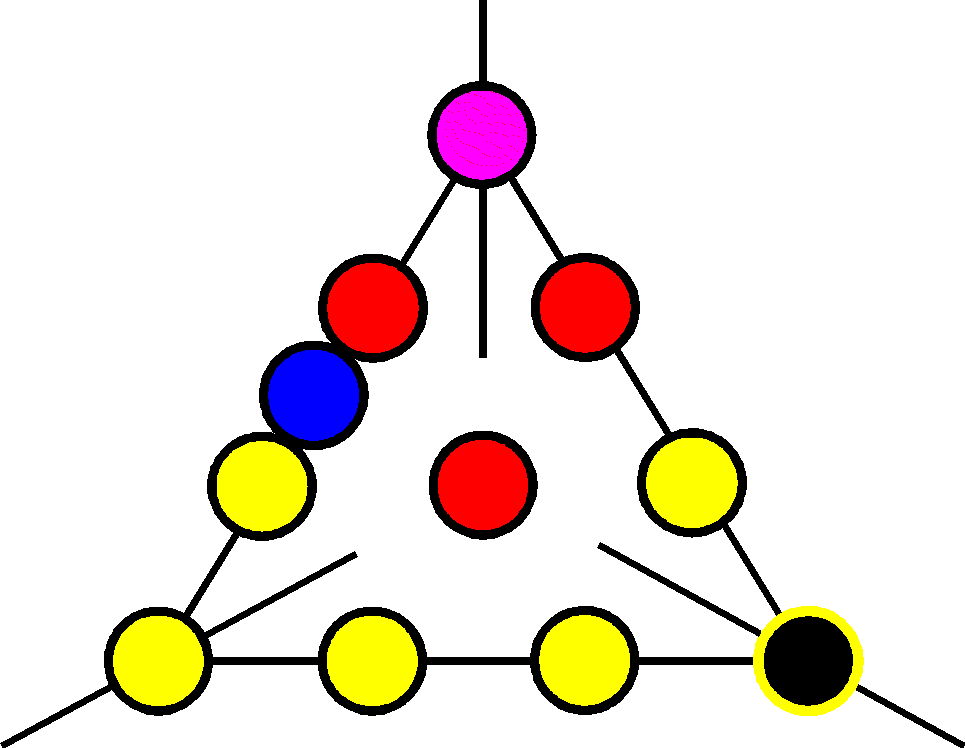
 Golden
ratio in the bank: Explaining the golden ratio by means of an
application. Pythagoras is known for Natural
(whole) numbers, triangular and square numbers, rationals and
irrationals —
and so we are going to derive and apply the golden ratio the
Pythagorean way
Golden
ratio in the bank: Explaining the golden ratio by means of an
application. Pythagoras is known for Natural
(whole) numbers, triangular and square numbers, rationals and
irrationals —
and so we are going to derive and apply the golden ratio the
Pythagorean way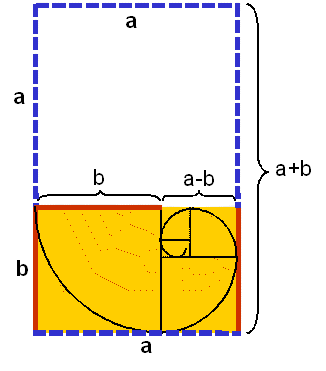









 QUANTUM
PYTHAGOREANS
QUANTUM
PYTHAGOREANS