Concept One: Momentum Creation	QM Gravitation, the Pythagorean approach
The first concept -- that of momentum -- is simple and easy. By definition, any moving body has momentum. Momentum can therefore be called the 'moving energy.' Energy is proportional to velocity square(d) and energy has but one value -- that of its magnitude. [This is true if you look at energy of a moving body. Eventually you'll figure out that energy exists in patterns.] Momentum is proportional to velocity and consequently momentum is a vector quantity as it has magnitude and direction (because velocity has magnitude and direction). The conservation of energy holds because the energy before and the energy after some operation are the same. Momentum is also conserved (it is moving energy), but momentum must be conserved as a vector. If momentum is conserved, then the only way to get things moving in the context of the conservation of momentum is to keep the momentum the same as found, even if it is zero. This seems like a riddle but if you have two bodies it can be done. You literally split the applied energy in half and apply both halves in the opposite direction to each body (bodies need not be of the same size). For angular momentum, the applied energy is also split in half, but it is the equal and opposite torque that is applied to both bodies (see below). As a Pythagorean you will recognize the number ½ (or 2) as the octave. As a mathematician, you will recall Riemann and his discovery of the "mysterious" number ½ when he worked the incomposite (prime) numbers. As a physicist you will know about the even wavefunction, which has its energy always evenly distributed about the axis, and thus the energies on the left and right of the axis are always the same. You will need to reduce the wavefunction to transform it and to realize (actualize, manifest) the energy. Because both bodies move away from a point at which they received the energy, the conservation of momentum must be happening along a one-dimensional line.	Math guys call a single value number the scalar number. Minimum Length Pythagoreans could call a 'vector' the wave number, for every wave carries a frequency and direction. Yes, each wave is nonlocal and must have direction -- both standing and moving waves have frequency (energy) and direction. In other words, a wave cannot exist as a point (hence it is nonlocal) and every 1D entity has a direction. You are smart and you are beginning to see how energy and a vector are tied together. Once we know a direction exists, we can then define a slope of a line (tangent). Does dy/dx -- the infinitesimal of Leibniz (bio) and Newton (bio) -- represent the direction, via a slope, of the shortest one-dimensional (1D) length there is? {May, 2007} More on this in the book. Also think about the mechanism of energy conservation a body must have once it accepts energy and begins to move. The mainstream scientist cannot envision the movement of a real object to have an underlying wave-based mechanism. This seems difficult only because the mainstream scientist [and you until now, perhaps] has a gap in the understanding of the mechanism that conserves energy. Yet, that is one of many things you will need to appreciate -- and move ahead. The conservation of energy holds from before to after some operation such as a collision or acceleration. Can we say that energy is conserved even after a transformation? If so, what would such tranformation be about? If energy is transformed and conserved, are we talking about the real and the virtual energy?   There is nothing better than turning science into art. We have a collection of designs inspired by the five pointed star. But if you look at the rings as orbitals you just might see how the electrons could be making the jumps. Enjoy select designs or visit our store at Zazzle (.com/Mike_Geo) too. You could look inspired and cool in a tee, a hoodie, or a long sleeve shirt. All designs come from nature and center on the golden proportion.
	To get things moving, we recognize two aspects: OneA. When two bodies are at rest, their mutual as well as their combined (total, system) momentum is zero. That is, the momentum vector is zero. OneB. When two bodies move in a particular way away or toward each other, their total momentum remains at zero and momentum is conserved. (Momentum vector is still zero.)
Aspect OneA: When two bodies are at rest, they are not moving with respect to each other. Their mutual momentum is zero because their respective velocities are zero. Momentum is a "punch," also called an impulse, which is a moving or a kinetic energy -- and if bodies are not moving there can be no mutual momentum no matter how one looks at it. We can then also erect a 3D boundary around both bodies and make a claim that inside this boundary the total (or combined) momentum is zero. We now have a system where the mutual momentum of both bodies is zero and the total (or combined) momentum of both bodies inside the boundary is zero as well.	System construction seems complex but the reason is that the mutual body-on-body interaction is happening along one dimension (usually motion), while the system boundary deals with other parameters that exist in three dimensions (usually energy). To a Pythagorean this is easy to appreciate because systems and system's parameters always operate in the framework of the Tetractys with zero, one, two, and three dimensions of freedom.
	Two points (two bodies) interact in one dimension
	Four points in space define volume in three dimensions
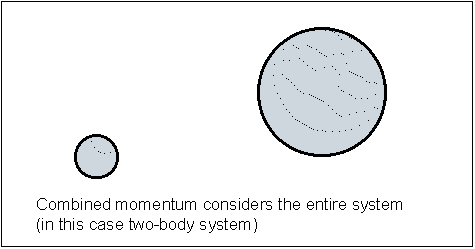
Aspect OneB: The particular way of moving two bodies is such that the energy imparted to one body is exactly equal to the energy that is imparted to the other body and always in the opposite direction. When these conditions are satisfied, both bodies can be brought to rest using only the energy imparted to them. That is, at any imaginable instance of time, one could bring these bodies to the initial condition while recovering the energy they already have. Once brought to rest, and although these bodies are farther apart, their mutual and their total (combined, system) momentum is zero. While the bodies are moving their system (total) momentum continues to be zero at all times even though their mutual momentum is not zero. That is why the system view consists of a contiguous 3D volume. You should also see that the two bodies need not be of the same size. When an equal amount of energy is given to both bodies, a larger body will move at a slower speed (indicated by a shorter arrow in the Illustration). The speed is indirectly proportional to the mass of the body. The product m1·v1 will be equal to m2·v2 because both bodies will have an equal amount of the moving energy. First conclusion: Spatial distance is not as important as some may think. Technically, getting from here to there takes no net energy at all. Energy Check: Whenever something moves, we need to account for energy such that the energy is always conserved. While it may appear strange that bodies subject to gravitation suddenly begin to move toward each other, the critical question deals with the conservation of energy. Whatever energy is used to move bodies (gravitation, explosive charge, photon absorption), this energy is conserved as momentum of the (now moving) bodies. The body (apple) is accelerating toward earth with the same energy as the earth is accelerating toward the body (apple) and in the opposite direction.	A body in motion can cause heat or create electrical energy. Because energy is always conserved then momentum is conserved. (Momentum differs from energy by a v/2 multiple where v is the velocity -- this was established by Leibniz (bio).) A moving energy that is momentum is also called the kinetic energy. Kinetic energy is real energy because it can be repeatably measured. All scientists think that real energy is the only form of energy. In the case of the so-called 'free energy,' for example, the scientist keeps looking for something that moves or wiggles because he or she is looking for real energy. Failing that, scientists are quick to make fools of themselves, for they cannot envision or explain virtual energy, which also exists and which must be transformed into real energy (in the framework of momentum conservation) if it is to manifest. You cannot, therefore, engage the mainstream or even a government scientist in the explanation of the virtual energy. You cannot ask for an endorsement of your 'new energy device' by a professor because he or she cannot give it to you. Yet, it can be worse. If you wish to pursue 'free energy' or 'new energy' work, you do not want to deal with the left brain lopsidedness of a professor or the government scientist, whose reality is to continue his payroll through your taxes. The freedom is always hard won and it will not be handed to you by a professor or an oilman.   The book you will thoroughly enjoy QUANTUM PYTHAGOREANS More ..
Therefore, if we apply energy in the particular way (split equally and in the opposite direction), we will always be able to return the energy in its entirety at any time. While the bodies are moving, the applied energy is conserved as a moving energy called momentum. The application of energy in this way, then, conserves energy in this two-body system at all times. Another way of saying it is that bodies within the system can have any amount of mutual momentum as long as the total momentum remains the same. Perhaps you know already that the particular way of applying energy to bodies is no other than the framework of the law of the conservation of momentum, which was first described by Galileo. Although Galileo and Newton established the conservation of momentum of bodies that are already in motion, we are now describing the creation and distribution of momentum. This means that we will get (at least two) bodies moving even though they might be at rest when we find them. Yes, this is new. We will postulate that Momentum cannot be created unless it can be distributed in the framework of momentum conservation Different ways of momentum distribution represent different potential solutions of momentum creation To create momentum in the framework of momentum conservation, at least two bodies are needed and a two-body system is the smallest system. Recall (Andre Ampere) that all gas molecules are composed of at least two atoms and, using photons, you can make much advancement in explaining gas pressure. What you may note as being new is that the spin can be included in the ways the momentum is created, in which case the overall linear speed slows down because some of the energy converts to rotational energy (second and third case in the Illustration above). Even though the solutions require that the total linear momentum is the same at all times and also that the total angular momentum is the same at all times, individual bodies gain linear and angular momentum. First question: Why should the spin be included in the solutions? [Think degrees of freedom and tractability because momentum-creating solution is about tractable computing]	In a school you likely studied the 'frame of reference.' There are even scientists who think that the movement of the object can be established only through a relative frame of reference because they think the absolute frame of reference is impossible.  Fortunately, Newton put energy first and qualitatively postulated that a movement of an object that was imparted with energy has the 'true motion' while the motion through a reference is but an 'apparent motion.' This is in his Principia. The energy imparted on a body gets it to move via inertia and the movement conserves the energy thus expended. In the dual slit experiment the moving energy (momentum) becomes a wave (de Broglie) and then Newton's absolute nature of spatial distance becomes demonstrative and provable because the placement of the frame of reference is not arbitrary in the dual-slit experiment. Applying the relative frame of reference is altogether worthless in the dual-slit experiment (QM primer) and in fact the dual slit experiment proves the fallacy of the relativistic presumption.  There are, then, such things as absolute rest and absolute speed and absolute spatial distance. It is not productive to deal with people (calling themselves scientists, too) who want to argue on the basis of ignorance and impossibilities when they claim that the absolute reference is not possible, particularly since "I don't know but someone else might" is not in their vocabulary. Not surprisingly the outcome of 'cannot do' or 'does not exist' foundation results in black holes, dark matter, dark energy, and similar incomplete concepts.
It is easier to use momentum in our description because momentum always has a direction associated with it. Opposite momentum becomes momentum that points in the opposite direction and this is simple enough to understand for either the linear or the angular momentum [if you have opposing thumbs, that is]. First exercise: If the linear and the angular momentum can be created together, are these coupled? That is, is there a coupling function such that a decrease in the angular momentum would result in a compensatory increase of the linear momentum? (This question leads to the heart of QM Gravitation. You may need to differentiate between spatial distance and space.) Now return to the First Question and you can add to it because we can now modulate or exchange linear and angular momentum. Also see DSSP Reports. Classically, the linear and the angular momentum are separate entities. Classically, we cannot equate the linear and angular momentum without transforming between the straight (Euclid) and curving (Riemann) geometries, and that is at the basis of the impossibility of NASA "Space Elevator." To understand this from yet another angle, consider what physical parameter is represented by the area of a circle. Second exercise: It is apparent we need to take the energy from somewhere. What needs to happen if energy is to appear? We know that once energy appears (once it manifests), we will be able to conserve it at all times. [This one is loaded. Think different forms of energy. Get esoteric. For example, does knowledge have value? If so, where is such knowledge stored? How can one extract such knowledge? How can one manifest such knowledge? Also think organization. Would it help if you can move more efficiently than the present bodies? Some people think better with symbols. In that case, think sliding on the moon's crescent.]
Second conclusion: Because the conservation of momentum holds, the total momentum in the entire universe is zero. Not a terribly exciting piece of information, but it is something we can say about the universe as a whole. This also makes sense as the universe is created 'out of nothing' -- that is, out of zero. What this also means is that, while the universe can be expanding, the universe as a whole is not moving and the universe as a whole is not translating or rotating. Third conclusion: You will always need energy when you want to get things moving. Theories that ignore that also ignore the conservation of energy. If a body gets moving because "space is warped," then you still need to know where the energy comes from. People talking about warped space or "fields" do so precisely because they do not know where the energy is coming from. Indeed, momentum (is real energy and) requires energy because there is no mo without energy. For small amounts of energy a photon will suffice nicely. Consider that photon's energy is evenly distributed (symmetrical) about its axis and a photon is an even function. The absorption of a photon, then, can create real momentum because photon's energy can be realized as two halves and applied in the opposite direction -- absorbed photon is "gone"; it has been transformed and its energy now lives as real (kinetic, electrical, pressure) energy. Yet another question: Which is more prevalent, linear or angular momentum? The angular mo is by far the most prevalent. 99% (or so) of the moving energy is stored as spin and rotation while a very small amount is in the form of the linear mo. You will note that a spin, rotation, or an orbit is a movement about a point (think geometry and radial symmetry.) Angular mo, moreover, permeates the scale from atomic to cosmic and so we have another page just on spin. You may give some thought to the link between inertia and the angular momentum [it's there]. Relating linear and angular momentum is even more important than you think so far. The orbit of the angular mo deals with curving geometry while the linear mo is on a straight path. So, these two different ways of storing the kinetic energy is also about the squaring of the circle, isn't it? A straightforward but the most insightful question is "how momentum affects a change in direction" or, similarly, why is the direction conserved or why is direction changed. These kinds of questions usually come up when analyzing collisions. The best way to understand direction is in the context of the conservation of energy. If you accelerate an object, you must have used spatial distance and, therefore, direction to do so (usually linear but also might be rotational). So, if the energy is conserved through the movement of the body, the direction comes with it. Leibniz was the first to figure it out (bio). If you want to get deeper into this, you want to start with the new definition/explanation of inertia. If you want to get even deeper into this [are you sure?], you will need to figure out the mechanism of storing moving energy and the existence and the role of ether. (The book Quantum Pythagoreans discusses the reason for the conservation of direction and also explains why such direction is absolute.) Momentum and impulse are the same. Equations are great to verify and understand the units of measure. For example, the equation F = m·a is the hallmark of classical physics. Because a = v/t (acceleration is a change in velocity over time), we can rewrite F = m·a as F·t = m·v and now you can see that impulse F·t is the same as momentum m·v.	QUANTUM PYTHAGOREANS When energy is imparted on an object, how does it stay with the object? How is energy conserved with the object and how does object's moving energy become a vector? You will find other energy properties such as a continuum in this book. Continue ..
"Yo Dad?" "Yo Alex." "When one body moves, it sends a signal to the other body. But that takes a while and the bodies will not sync up to conserve momentum at all times." "That sure is the classical way of looking at it. Quantum mechanically, wavefunctions exist in superposition, one together with all the others, and they interconnect both bodies. When some wavefunctions instantly reduce, each body receives an equal and opposite amount of momentum." "But that means that momentum appears out of, ..nothing. That means that there is some knowledge out there that figures out how much momentum should appear -- and when and where it should appear!" "Yeah. No big deal." "Hold your quantum leaping lizards, Pops. Nothing can go faster than the speed of light." "Quite so. When two mass bodies are moving, they do it below the speed of light. Wavefunctions relate to each other at the speed of light and they can easily keep up. When wavefunctions correlate -- that is, when they compute -- there exists a potential for momentum realization that is constantly changing at the speed of light; yet it is only a potential. When the wavefunction does reduce, it happens instantly and the imparting of momentum to both bodies is instantaneous. The information is in place already -- actually at both places already." "If I think about a planet and how it can change path going around in the elliptical orbit and how it can speed up and slow down and speed up again, then there must be some momentum increase and decrease." "That's it! The orbit can be described with an equation but you are thinking about the mechanics that bring it about. Let's take a step back so that we can move two steps ahead. Have a look at a batch of topics as Concept Two." Then of course we recall Newton and his instant action of equal and opposite force because force cannot arise as one-sided force.
QUANTUM PYTHAGOREANS  Book by Mike Ivsin Even and odd symmetry is something that separates masculine and feminine. Technical and esoteric aspects broaden out your understanding of the building and organizing concepts. You will also find out what happens instantly and what does not, and why. Going well beyond gravitation and into self-organization, the forces are everywhere, including the pyramid. You will understand the virtual domain, the transformative mechanism, and the harmonious compositions of the true reality. Continue ..
Go or select another topic from the gold post HyperFlight home Portal in new window © 2000-7, 2010, 2013 Backbone Consultants. Copyrights Information Last update May 31, 2013